AI4R's final project was a bit different than you might expect... In fact, we were asked to track and predict the motion of an object that care barely be called a "robot" at all - a HEXBUG (Example on YouTube). Somebody at GT (presumably) constructed a wooden box for the robot, and then put a circular candle in the center as an obstacle. A video camera was mounted above the scene, and they put the hexbug in and recorded the results. Our job was to accept 60 seconds of this motion and then predict the hexbug's path over the following 2 seconds.
We were given both the video files and a csv of extracted coordinates of the hexbug. This was real-world data, and the extracted coordinates were very messy, so teams were free to do their own analysis of the video. Also, given that this was a real physical experiment in the physical world, there might be irregularities in the environment that teams could exploit. Maybe there's a dip in the wood base that causes a right turn at some point more frequently than a left, for example. There were many such rabbit holes one could venture down...
There are two different tasks involved in this project. At first, it is a tracking problem with noisy input. Then, it becomes a prediction problem with no feedback loop. So on our team, we tacked each problem with different approaches.
Tracking the bot wasn't actually too hard - a standard Kalman filter can do the job, as the motion can be modeled as linear. The only trick is handle collisions - if you don't model these, your KF will average out over time to a nearly-zero dx/dy - no good! We approached the problem by applying some pretty naive "billiards-style" physics to the bot, and using that to generate a u (external force or motion control) vector if a collision was predicted to occur. This worked pretty well, even though our model of the physics was not great compared to what the hexbug actually did: never went straight, got stuck in corners for an indeterminant amount of time, was modeled like a circle when it was really a rectangle, etc. Still, we were tracking the object well enough to move on, thanks to the Kalman filter incorporating these errors well.
Our predictions were going to be what we were graded on, so it made sense to focus more effort in this area. We entered the prediction stage with a good estimate of the hexbug's state, as output from the Kalman filter. A a baseline, we can iteratively predict and handle collisions from that same KF. This served as our baseline prediction algorithm. It didn't do badly, but was sensitive to small variations in state before a bounce leading to big possible errors in course after the bounce.
Enter "Probabilistic Robotics," the textbook by Sebastian Thrun, Wolfram Burgard, and Dieter Fox that this course was based around. The common thread to all ideas in the book is to admit that there is uncertainty in measurement and the robot's belief about its state, and to incorporate that in the model and algorithms used to compute or predict state. Work with it, not against it, in other words. Chapter five deals with robot motion, and suggests the idea of using a particle filter to predict future motion. Since the motion has some uncertainty associated with it, each particle moves to a slightly-different place after each motion step:
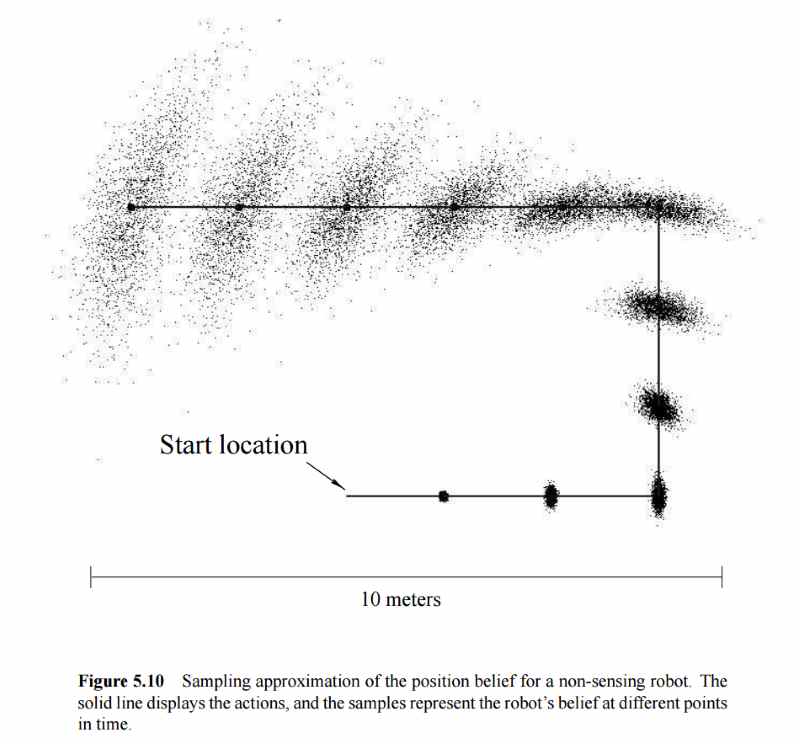Especially when there are obstacles in the environment, some of your particles may interact with them when others don't - and this possibility of interaction is then modeled. Neat trick. So again we can use that some bounce code from before to throw our particles at. We produced our predicted locations by simply averaging the locations of the particle cloud.
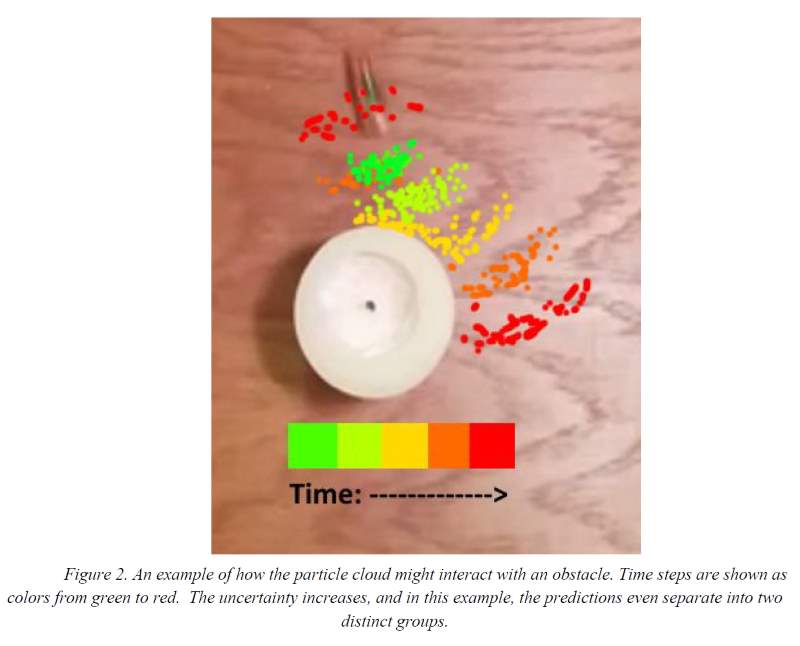
How much uncertainty should we use for the motion? We developed the algorithm with a completely naive guess, then tried to get fancy and analyze the training data to get a better guess. We got a lower number, and plugged this in, and to my great surprise, got a worse error rate out from our predictions. This was totally baffling to me until I read the following quote from the intro to chapter five in Probabilistic Robotics:
"In theory, the goal of a proper probabilistic model may appear to accurately model the specific types of uncertainty that exist in robot actuation and perception. In practice, the exact shape of the model often seems to be less important that the fact that some provisions for uncertain outcomes are provided in the first place. In fact, many of the models that have proven most successful in practical applications vastly overestimate the amount of uncertainty. By doing so, the resulting algorithms are more robust to violations of the Markov assumptions, such as unmodeled state and the effect of algorithmic approximations." (p. 118)
I love it when stuff like that happens.
I'd like to share my project report here, but I'm not actually sure I can for academic integrity reasons. They are some serious folks over at Georgia Tech. I am fairly-certain just talking about approaches in the general sense on this blog is a-okay, however, so that might be all you get.