Stupid Computer Tricks - Best Hiking Path

The Problem

How would you approach finding a good hiking route from the trailhead to the summit, given a digital elevation model (DEM) of the terrain? I defined a "good" route based on my own experiences - shorter distances are better than longer, going up is a lot harder than going straight, and going down is hard on the knees. Given these assumptions, we can compute a concrete cost from one pixel in the DEM to one of it's neighbors. Now, call each pixel a vertex and each cost an edge with a weight, and we have a graph we can run shortest path algorithms on.

I chose a hike I did in the Maroon Bells-Snowmass Wilderness in Colorado to test this one. I had (spotty) GPS data from my hiking app of my actual route taken. The hike region was split across 2 DEMs from the USGS's National Map system 1/3 arcsecond 3DEP project. These are seamless data products, so they could simply be concatenated together and then cropped to the region of interest without too much trouble.

Solution

Directly creating this graph would be expensive in time and memory, and is actually completely unnecessary. Djikstra's algorithm doesn't actually require a graph object, it just needs a data structure that implements operations like "neighbors" and "distance." I wrote a wrapper around the raster DEM itself to return edges with weights from any given vertex, and plugged this in to Djikstra's, rememberd each previous vertex, and presto, we have a path.

Neighbors are all adjacent pixels, including diagonals. Costs are computed based on the distance between the two pixels, plus the vertical change (that's distance too), and then extra penalties based on how much vertical up or down took place. The down penalty is less than and proportional to the upward movement penalty. It's easier to go down than it is to go up, but my knees will tell you that it is definitely not free.

Results

Running this iteratively over a range of vertical-hike penalties and plotting the results mirror what you might expect in the real world nicely. If there is no extra cost for vertical changes, we straight lines and diagoals moving more-or-less directly to the goal - even if we have to climb and descend a peak to do it. Adding in a little bit of vertical penalty starts to yield paths that look more... sensible.

My hike in Colorado reached two separate summits - first one to the East, then tracking back Northwest. I ran the pathfinding code with both of them as endpoints. You can see the results below, with my actual recorded hiking path underlayed in gray.

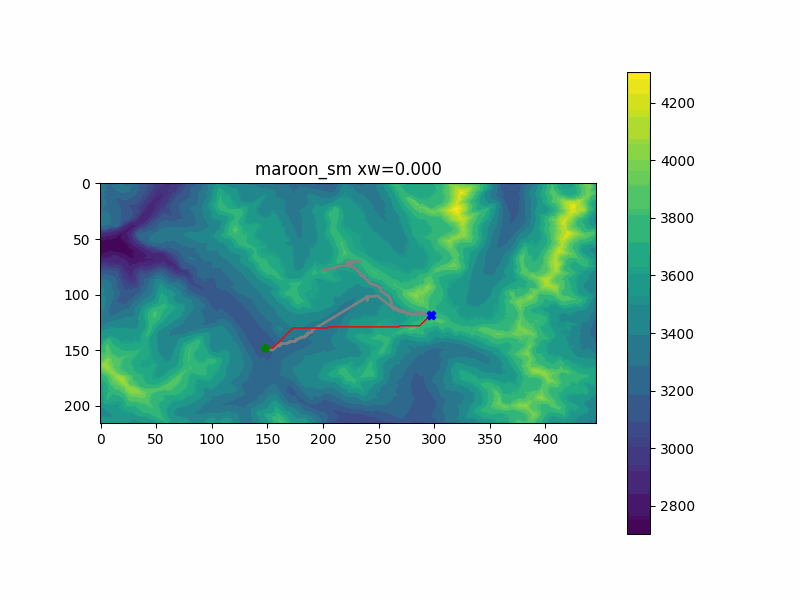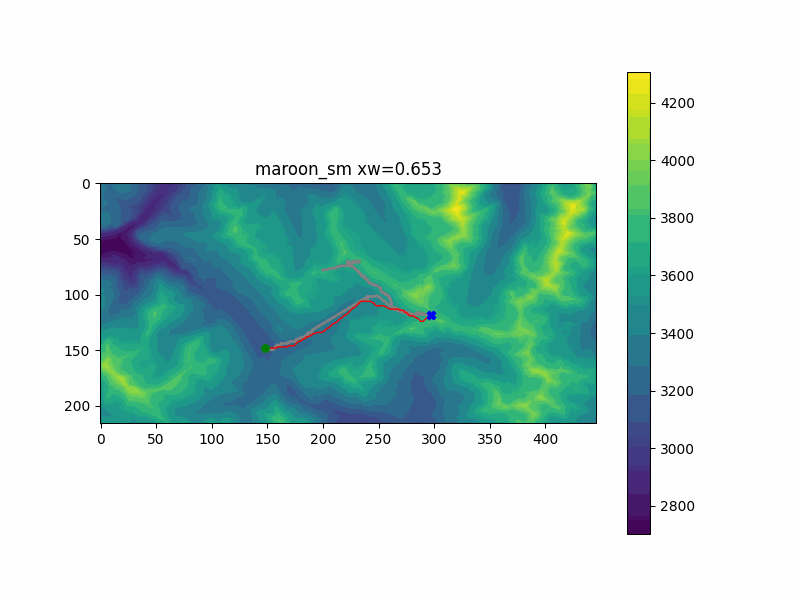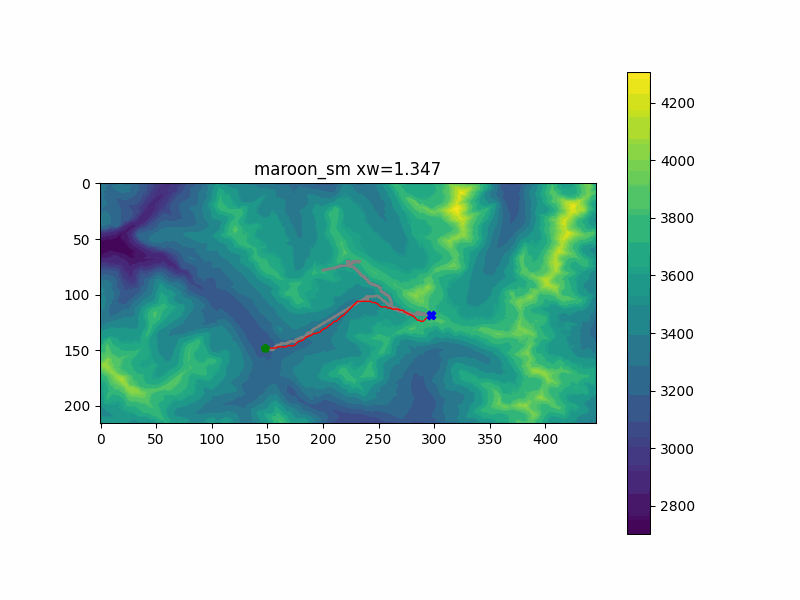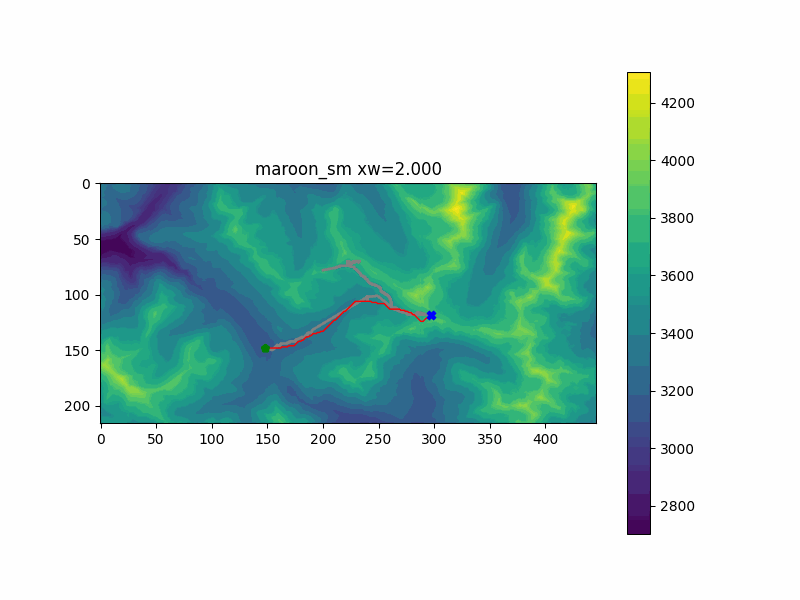
The first peak was simulated in the "maroon_sm" run. My favorite part of this run was the change between zw=0.204 and zw=0.245. At this point, adding just a little extra cost to the vertical climb penalty changed the route to go further out of the way to stay on flatter ground - just as the actual hiking trail does as well. This is likely close to optimal, since the route doesn't significantly change after that.

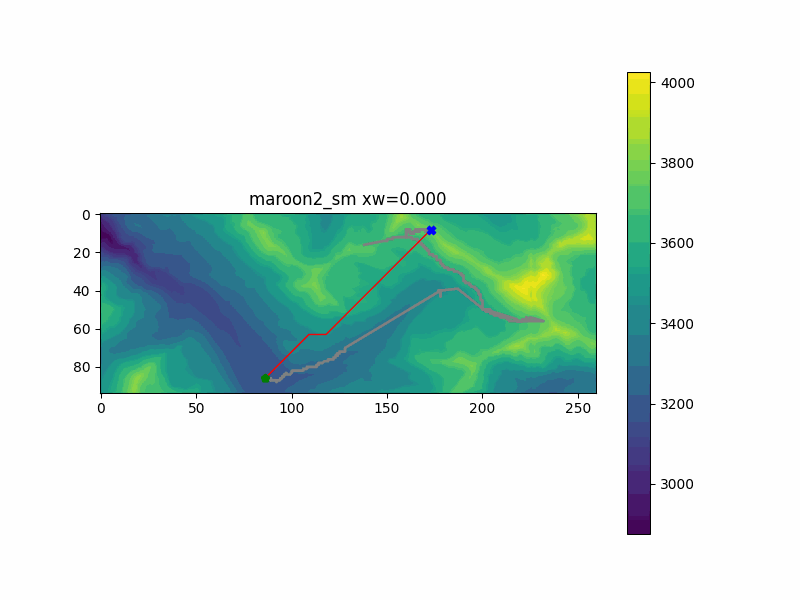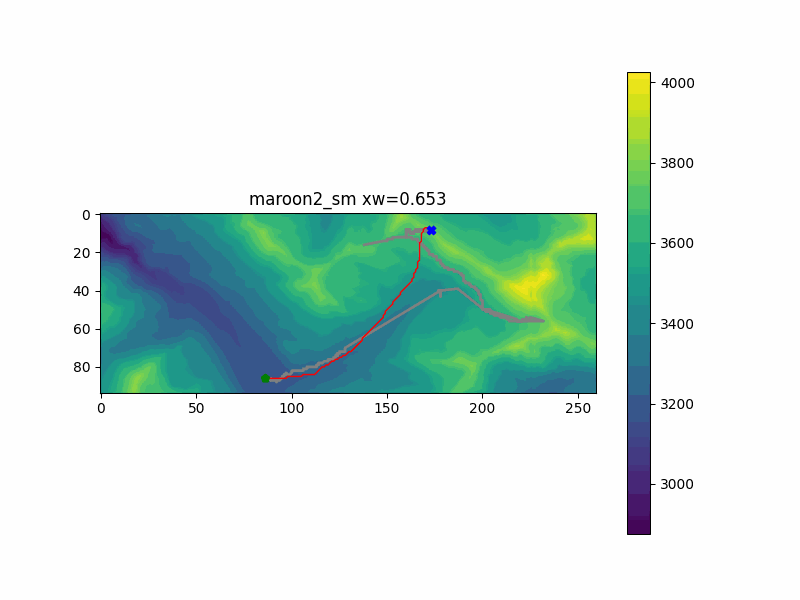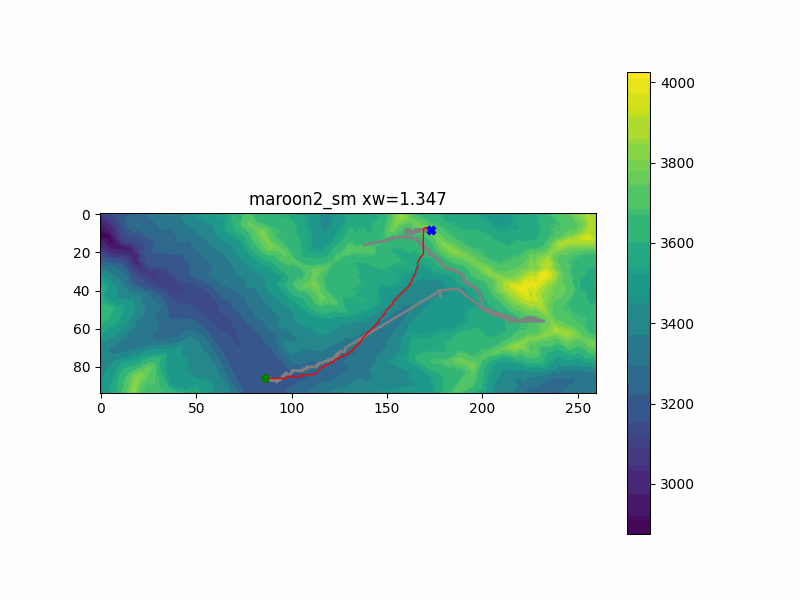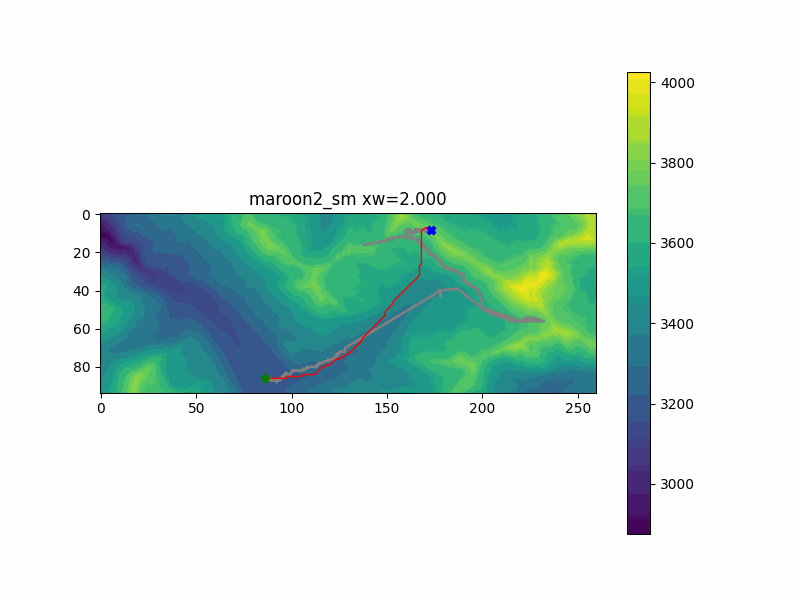
The second peak, illustrated by the run "maroon2_sm" doesn't have the same ground truth route that the first peak did. I can't directly compare what route I would have taken to get to that peak directly, since I visited the first peak on the way. But I can guarantee I would not have followed the first result the code gives us, when it assumes we don't care about vertical changes. The route goes over the mountain and back down to ge there. But again, we converge on a sensible solution pretty early, going around the mountain. There are some refinements made about exactly how to get up to the top, and how far to divert around the mountain in the middle, but we get a pretty good solution pretty fast.

Applications

I could see this being used to path plan characters in video games in similar rugged terrain. It wouldn't have to be done at a very high resolution to give the characters the appearance of taking sensible routes around the world - even if there are no trails manually marked in the environment. Each character could be initialized with a random value for vertical cost (maybe sampled based on another strength value, etc) and then multiple characters in the environment would all take slightly different paths toward the goal. This may give an attacking army an interesting dynamism, for example.

If you are planning a big hike yourself, or new trails are being planned in a new National Park - obviously this could give managers a starting point for where how to route the trails, especially if they haven't seen the area directly.

Possible Improvements

• Command line interface with Click to make interactive use easier.
• Build in a vertical cost that exponentially weights the vertical change. This would make a long flat path followed by a steep ascent harder than a slow steady ascent over the same distance. I wonder if this would generate switchback paths so often seen in real hiking trails?
• Perform some sort of clustering on the terrain model to simplify the graph. As it stands now, the graphs grow very large as image dimensions grow, even if most points are very similar to their neighbors in this case. If many nearby verteces of a similar elevation could be collapsed into one vertex, where it makes sense to do so, larger areas could be computed without significantly affecting the outcome.

Summmary

I hope you found this somewhat interesting. It's not groundbreaking, it's just an excuse to do some casual experiments on different kinds of data.

A GitHub repo for this project can be found here.